DCF Myth 3.2: If you don't look, its not there!

In this, the last of my three posts on uncertainty, I complete the cycle I started with a look at the responses (healthy and unhealthy) to uncertainty and followed up with an examination of the Margin of Safety, by taking a more extended look at one approach that I have found helpful in dealing with uncertainty, which is to run simulations. Before you read this post, I should warn you that I am not an expert on simulations and that the knowledge I bring to this process is minimalist and my interests are pragmatic. So, if you are an expert in statistics or a master simulator, you may find my ramblings to be amateurish and I apologize in advance. 

Setting the Stage

The tools that we use in finance were developed in simpler times, when data was often difficult (or expensive) to access and sophisticated statistical tools required machine power that was beyond the reach of most in the finance community. It should come as no surprise then that in discounted cash flow valuation, we have historically used point estimates ( single numbers that reflect best judgments at the time of the valuation) for variables that have probability distributions attached to them. To illustrate, in my valuation of Apple in February 2016, I used a revenue growth rate of 2.2% and a target operating margin of 25%, to arrive at my estimate of value per share of $129.80.

It goes without saying (but I will say it anyway) that I will be wrong on both these numbers, at least in hindsight, but there is a more creative way of looking at this estimation concern. Rather than enter a single number for each variable, what if I were able to enter a probability distribution? Thus, my estimate for revenue growth would still have an expected value of 2.2% (since that was my best estimate) but would also include a probability distribution that reflected my uncertainty about that value. That distribution would capture not only the magnitude of my uncertainty (in a variance or a standard deviation) but also which direction I expect to be wrong more often (whether the growth is more likely to be lower than my expected value or higher).  Similarly, the expected value for the operating margin can stay at 25% but I can build in a range that reflects my uncertainty about this number.

Once you input the variables as distributions, you have laid the foundations for a probabilistic valuation or more specifically, for a simulation, where in each run, you pick one outcome out of each distribution (which can be higher or lower than your expected values) and estimate a value for the company based on the drawn outcomes. Once you have run enough simulations, your output will be a distribution of values across simulations. If the distributions of your variables are built around expected values that match up to the numbers that you used in your point estimate valuation, the expected value across the simulations will be close to your point estimate value. That may seem to make the simulation process pointless, but there are side benefits that you get from simulations that enrich your decision process. In addition to the expected value, you will get a measure of how much variability there is in this value (and thus the risk you face), the likelihood that you could be wrong in your judgment of whether the stock is under and over valued and the potential payoffs to be right and wrong. 

Statistical Distributions: A Short Preview

It is a sad truth that most of us who go through statistics classes quickly consign them to the “I am never going to use this stuff” heap and move on, but there is no discipline that is more important in today’s world of big data and decision making under uncertainty. If you are one of those fortunate souls who not only remembers your statistics class fondly but also the probability distributions that you encountered during the class, you can skip this section. If, like me, the only memory you have of your statistics class is of a bell curve and a normal distribution, you need to expand your statistical reach beyond a normal distribution, because much of what happens in the real world (which is what you use probability distributions to capture) is not normally distributed. At the risk of over simplifying the choices, here are some basic classifications of uncertainties/ risks::

1. Discrete versus Continuous Distributions: Assume that you are valuing an oil company in Venezuela and that you are concerned that the firm may be nationalized, a risk that either occurs or does not, i.e., a discrete risk. In contrast, the oil company's earnings will move with oil prices but take on a continuum of values, making it a continuous risk. With currency risk, the risk of devaluation in a fixed exchange rate currency is discrete risk but the risk in a floating rate currency is continuous.
2. Symmetric versus Asymmetric Distributions (Symmetric, Positive skewed, Negative skewed): While we don't tend to think of upside risk, risk can deliver outcomes that are better than expected or worse than expected. If the magnitude and likelihood of positive outcomes and negative outcomes is similar, you have a symmetric distribution. Thus, if the expected operating margin for Apple is 25% and can vary with equal probability from 20% to 30%, it is symmetrically distributed. In contrast, if the expected revenue growth for Apple is 2%, the worse possible outcome is that it could drop to -5%, but there remains a chance (albeit a small one) that revenue growth could jump back to 25% (if Apple introduces a disruptive new product in a big market), you have an a positively skewed distribution. In contrast, if the expected tax rate for a company is 35%, with the maximum value equal to the statutory tax rate of 40% (in the US) but with values as low as 0%, 5% or 10% possible (though not likely), you are looking at a negatively skewed distribution.
3. Extreme outcome likelihood (Thin versus Fat Tails): There is one final contrast that can be drawn between different risks. With some variables, the values will be clustered around the expected value and extreme outcomes, while possible, don't occur very often; these are thin tail distributions. In contrast, there are other variables, where the expected value is just the center of the distribution and actual outcome that are different from the expected value occur frequently, resulting in fat tail distributions.

I know that this is a very cursory breakdown, but if you are interested, I do have a short paper on the basics of statistical distributions (link below), written specifically with simulations in mind. 

Simulation Tools

I was taught simulation in my statistics class, the old fashioned way. My professor came in with three glass jars filled with little pieces of paper, with numbers written on them, representing the different possible outcomes on each variable in the problem (and I don't even remember what the problem was). He then proceeded to draw one piece of paper (one outcome) out of each jar and worked out the solution, with those numbers and wrote it on the board. I remember him meticulously returning those pieces of paper back into the jar (sampling with replacement) and at the end of the class, he proceeded to compute the distribution of his solutions.

While the glass jar simulation is still feasible for simulating simple processes with one or two variables that take on only a few outcomes, it is not a comprehensive way of simulating more complex processes or continues distributions. In fact, the biggest impediment to using simulation until recently would have been the cost of running one, requiring the use of a mainframe computer. Those days are now behind us, with the evolution of technology both in the form of hardware (more powerful personal computers) and software. Much as it is subject to abuse, Microsoft Excel has become the lingua franca of valuation, allowing us to work with numbers with ease. There are some who are conversant enough with Excel's bells and whistles to build simulation capabilities into their spreadsheets, but I am afraid that I am not one of those. Coming to my aid, though, are offerings that are add-ons to Excel that allow for the conversion of any Excel spreadsheet almost magically into a simulation.

I normally don't make plugs for products and services, even if I like them, on my posts, because I am sure that you get inundated with commercial offerings that show up insidiously in Facebook and blog posts. I am going to make an exception and praise Crystal Ball, the Excel add-on that I use for simulations. It is an Oracle product and you can get a trial version by going here. (Just to be clear, I pay for my version of Crystal Ball and have no official connections to Oracle.) I like it simply because it is unobtrusive, adding a menu item to my Excel toolbar, and has an extremely easy learning curve.

My only critique of it, as a Mac user, is that it is offered only as a PC version and I have to run my Mac in MS Windows, a process that I find painful. I have also heard good things about @Risk, another excel add-on, but have not used it.

Simulation in Valuation

There are two aspects of the valuation process that make it particularly well suited to Monte Carlo simulations. The first is that uncertainty is the name of the game in valuation, as I noted in my first post in the series. The second is that valuation inputs are often estimated from data, and that data can be plentiful at least on some variables, making it easier to estimate the probability distributions that lie at the heart of simulations. The sequence is described in the picture below:

Step 1: Start with a base case valuation
The first place to start a simulation is with a base case valuation. In a base case valuation, you do a valuation with your best estimates for the inputs into value from revenue growth to margins to risk measures. Much as you will be tempted to use conservative estimates, you should avoid the temptation and make your judgments on expected values. In the case of Apple, the numbers that I use in my base case valuation are very close to those that I used just a couple of months ago, when I valued the company after its previous earnings report and are captured in the picture below:

Download spreadsheet

In my base case, at least, it looks like Apple is significantly under valued, priced at $93/share, with my value coming in at $126.47, just a little bit lower my valuation a few months ago. I did lower my revenue growth rate to 1.50%, reflecting the bad news about revenues in the most recent 10Q.

Step 2: Identify your driver variables

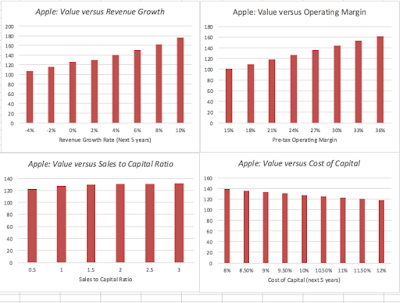
While there are multiple inputs into valuation models that determine value, it remains true that a few of these inputs drive value and that the rest go along for the ride. But how do you find these value drivers? There are two indicators that you can use. The first requires trial and error, where you change each input variable to see which ones have the greatest effect on value. It is one reason that I like parsimonious models, where you use fewer inputs and aggregate numbers as much as you can. The second is more intuitive, where you focus on the variable that investors in the company seem to be most in disagreement about. My Apple valuation is built around four inputs: revenue growth (growth), operating margin (profitability), the sales to capital ratio (investment efficiency) and cost of capital (risk). The graph below captures how much value changes as a function of these inputs:

As you can see the sales to capital ratio has little effect on value per share, largely because the base case growth rate that I use for Apple is so low. Revenue growth and operating margin both affect value significantly and cost of capital to a much lesser degree. Note that the value per share is higher than the current price though every single what-if analysis, but that reflects the fact that only variable at a time in being changed in this analysis. It is entirely possible that if both revenue growth and operating margins drop at the same time, the value per share will be lower than $93 (the stock price at the time of this analysis) and one of the advantages of a Monte Carlo simulation is that you can build in interconnections between variables. Looking at the variables through the lens that investors have been using to drive the stock price down, it seems like the front runner for value driver has to be revenue growth, as Apple reported its first year on year negative revenue growth in the last quarter and concerns grow about whether the iPhone franchise is peaking. Following next on the value driver list is the operating margin, as the competition in the smart phone business heats up.

Step 3: The Data Assessment

Once you have the value drivers identified, the next step is collecting data on these variables, as a precursor for developing probability distributions. In developing the distributions, you can draw on the following:

1. Past data: If the value driver is a macroeconomic variable, say interest rates or oil prices, you can draw on historical data going back in time. My favored site for all things macroeconomic is FRED, the Federal Reserve data site in St. Louis, a site that combines great data with an easy interface and is free. I have included data on interest rate, inflation, GDP growth and the weighted dollar for those of you interested in US data in the attached link. For data on other countries, currencies and markets, you can try the World Bank data base, not as friendly as FRED, but rich in its own way.
2. Company history: For companies that have been in existence for a long time, you can mine the historical data to get a measure of how key company-specific variables (revenues, operating margin, tax rate) vary over time. 
3. Sector data: You can also look at cross sectional differences in key variables across companies in a sector. Thus, to estimate the operating margin for Amazon, you could look at the distribution of margins across retail companies.: If the value driver is a macroeconomic variable, say interest rates or oil prices, you can draw on historical data going back in time. My favored site for all things macroeconomic is FRED, the Federal Reserve data site in St. Louis, a site that combines great data with an easy interface and is free. I have included data on interest rate, inflation, GDP growth and the weighted dollar for those of you interested in US data in the attached link. For data on other countries, currencies and markets, you can try the World Bank data base, not as friendly as FRED, but rich in its own way.

In the case of Apple, I isolated my data assessment to three variables: revenue growth, operating margin and the cost of capital.  To get some perspective on the range and variability in revenue growth rates and operating margins, I started by looking at the values for these numbers annually from 1990 to 2015:

This extended time period does distract from the profound changes wrought at Apple over the last decade by the iPhone. To takes a closer look at its effects, I looked at growth and margins at Apple for every quarter from 2005 to the first quarter of 2016 :

Superimposed on this graph of gyrating revenue growth, I have traced the introduction of the different iPhone models that have been largely responsible for Apple's explosive growth over the last decade. There are a few interesting patterns in this graph. The first is that revenue growth is clearly driven by the iPhone cycle, peaking soon after each new model is introduced and fading in the quarters after. The second is that the effect of a new iPhone on revenue growth has declined with each new model, not surprising given the scaling up of revenues as a result of prior models. The third is that the operating margins have been steady through the iPhone cycles, with only a midl dip in the last cycle. There is good news and bad news in this graph for Apple optimists. The good news is that the iPhone 7 will deliver an accelerator to the growth but the bad news is that it will be milder that the prior versions; if the trend lines hold up, you are likely to see only a 10-15% revenue growth in the quarters right after its introduction. 

To get some perspective on what the revenue growth would look like for Apple, if it's iPhone franchise fades, I looked at the compounded annual revenue growth for US technology firms older than 25 years that were still listed and publicly traded in 2016:

Of the 343 firms in the sample, 26.2% saw their revenues decline over the last 10 years. There is a sampling bias inherent in this analysis, since the technology firms with the worst revenue growth declines over the period may not have survived until 2016. At the same time, there were a healthy subset of aging technology firms that were able to generate revenue growth in the double digits over a ten-year period. 

Step 4: Distributional Assumptions
There is no magic formula for converting the data that you have collected into probability distributions, and as with much else in valuation, you have to make your best judgments on three dimensions.

1. Distribution Type: In the section above, I broadly categorized the uncertainties you face into discrete vs continuous, symmetric vs skewed and fat tail vs thin tail. At the risk of being tarred and feathered for bending statistical rules, I have summarized the distribution choices based on upon these categorizations. The picture is not comprehensive but it can provide a road map though the choices:
   
2. Distribution Parameters: Once you have picked a distribution, you will have to input the parameters of the distribution. Thus, if you had the good luck to have a variable be normally distributed, you will only be asked for an expected value and a standard deviation. As you go to more complicated distributions, one way to assess your parameter choices to look at the full distribution, based upon your parameter choices, and pass it through the common sense test.

In the case of Apple, I will use the historical data from the company, the cross sectional distribution of revenue growth across older technology companies as well as a healthy dose of subjective reasoning to pick a lognormal distribution, with parameters picked to yield values ranging from -4% on the downside to +10% on the upside. On the target operating margin, I will build my distribution around the 25% that I assumed in my base case and assume more symmetry in the outcomes; I will use a triangular distribution to prevent even the outside chance of infinite margins in either direction.

Note the correlation between the two, which I will talk about in the next section.

Step 5: Build in constraints and correlations
There are two additional benefits that come with simulations. The first is that you can build in constraints that will affect the company's operations, and its value, that are either internally or externally imposed. For an example of an external constraint, consider a company with a large debt load. That does not apply to Apple but it would to Valeant. If the company's value drops below the debt due, you could set the equity value to zero, on the assumption that the company will be in default. As another example, assume that you are valuing a bank and that you model regulatory capital requirements as part of your valuation. If the regulatory capital drops below the minimum required, you can require the company to issue more shares (thus reducing the value of your equity).  The second advantage of a simulation is that you can build in correlations across variables, making it more real life. Thus, if  you believe that bad outcomes on margins (lower margins than expected) are more likely to go with bad outcomes on revenue growth (revenue growth lower than anticipated), you can build in a positive correlation between the variables. With Apple, I see few binding constraints that will affect the valuation. The company has little chance of default and is not covered by regulatory constraints on capital. I do see revenues and operating margins moving together and I build in this expectation by assuming a correlation of 0.50 (lower than the historical correlation of 0.61 between revenues and operating margin from 1989 to 2015 at Apple).

Step 6: Run the simulations

Using my base case valuation of Apple (which yielded the value per share of $126.47) as my starting point and inputting the distributional assumptions for revenue growth and operating margin, as well as the correlation between the two, I used Crystal Ball to run the simulations (leaving the number at the default of 100,000) and generated the following distribution for value:

The percentiles of value and other key statistics are listed on the side. Could Apple be worth less than $93/share. Yes, but the probability is less than 10%, at least based on my assumptions. Having bought and sold Apple three times in the last six years (selling my shares last summer), this is undoubtedly getting old, but I am an Apple shareholder again. I am not a diehard believer in the margin of safety, but if I were, I could use this value distribution to create a more flexible version of it, increasing it for companies with volatile value distributions and reducing it for firms with more stable ones.

The most serious concern that I have, as an investor, is that I am valuing cash , which at $232 billion is almost a third of my estimated value for Apple, as a neutral asset (with an expected tax liability of $28 billion). Some of you, who have visions of Apple disrupting new businesses with the iCar or the iPlane may feel that this is too pessimistic and that there should be a premium attached for these future disruptions. My concern is the opposite, i.e., that Apple will try to do too much with its cash, not too little. In my post on aging technology companies, I argued that, like aging movie stars in search of youth, some older tech companies throw money at bad growth possibilities. With the amount of money that Apple has to throw around, that could be deadly to its stockholders and I have to hope and pray that the company remains restrained, as it has been for much of the last decade.

Conclusion

Uncertainty is a fact of life in valuation and nothing is gained by denying its existence. Simulations offer you an opportunity to look uncertainty in the face, make your best judgments and examine the outcomes. Ironically, being more open about how wrong you can be in your value judgments  will make you feel more comfortable about dealing with uncertainty, not less. If staring into the abyss is what scares you, take a peek and you may be surprised at how much less scared you feel.

YouTube video


Attachments

1. Paper on probability distributions
2. Apple valuation - May 2016
3. Link to Oracle Crystal Ball trial offer

Uncertainty Posts

1. DCF Myth 3: You cannot do a valuation, when there is too much uncertainty
2. The Margin of Safety: Excuse for Inaction or Tool for Action?
3. Facing up to Uncertainty: Probabilities and Simulations

DCF Myth Posts
Introductory Post: DCF Valuations: Academic Exercise, Sales Pitch or Investor Tool

1. If you have a D(discount rate) and a CF (cash flow), you have a DCF.  
2. A DCF is an exercise in modeling & number crunching. 
3. You cannot do a DCF when there is too much uncertainty.
4. The most critical input in a DCF is the discount rate and if you don’t believe in modern portfolio theory (or beta), you cannot use a DCF.
5. If most of your value in a DCF comes from the terminal value, there is something wrong with your DCF.
6. A DCF requires too many assumptions and can be manipulated to yield any value you want.
7. A DCF cannot value brand name or other intangibles. 
8. A DCF yields a conservative estimate of value. 
9. If your DCF value changes significantly over time, there is something wrong with your valuation.
10. A DCF is an academic exercise.

DCF Myth 3.1: The Margin of Safety - Tool for Action or Excuse for Inaction?

In my last post on dealing with uncertainty, I brought up the margin of safety, the tool that many value investors claim to use to protect themselves against uncertainty. While there are certainly some in the value investing community who have found a good way to incorporate MOS into their investing process, there are many more who seem to have misconceptions about what it does for them as well as the trade off from using it. 

The Margin of Safety: Definition and Rationale

While the margin of safety has always been around, in one form or another, in investing, it was Ben Graham who brought the term into value investing in The Intelligent Investor, when he argued that the secret of sound investment is to have a margin of safety, with the margin of safety defined as the difference between the value of an asset and its price. The definitive book on MOS was written by Seth Klarman, a value investing icon. Klarman’s book has acquired a cult following, partly because of its content and partly because it has been out of print now for years; a quick check of Amazon indicates a second-hand copy can be acquired for about $1600. Klarman’s take on margin of safety is similar in spirit to Graham’s measure, with an asset-based focus on value, which is captured in his argument that investors gain the margin of safety by “buying at a significant discount to underlying business value and giving preference to tangible assets over intangibles”.

There are many reasons offered for maintaining a margin of safety. The first is that the value of an asset is always measured with error and investors, no matter how well versed they are in valuation techniques, have to recognize that they can be wrong in their judgments. The second is that the market price is determined by demand and supply and if it diverges from value, its pathway back is neither quick nor guaranteed. The proponents of margin of safety point to its benefits. By holding back on making investment decisions (buy or sell) until you feel that you have a margin of safety, they argue that you improve your odds of making successful investments. In addition, They also make the point that having a healthy margin of safety will reduce the potential downside on your investments and help protect and preserve your capital. 

The Margin of Safety: Divergence across Investors

As a concept, I not only understand the logic of the MOS, but also its allure, and I am sure that many investors adopt some variant of it in active investing, but there are differences in how it is employed:

1. Valuation Basis: While MOS is often defined it as the difference between value and price, the way in which investors estimate value varies widely. The first approach is intrinsic value, either in its dividend discount model format or a more expansive DCF version. The second approach estimates value from accounting balance sheets, using either unadjusted book value or variants thereof (tangible book value, for instance). The third approach is to use a pricing multiple (PE, EV to EBITDA), in conjunction with peer group pricing, to estimate “a fair price” for the company. While I would contest even calling this number a value, it is still used by many investors as their estimated value.
2. Magnitude and Variability: Among investors who use MOS in investing, there seems to be no consensus on what constitutes a sufficient margin. Even among investors who are explicit about their MOS, the follow up question becomes whether it should be a constant (say 15% for all investments) or whether it should be greater for some investments (say in risky sectors or growth stocks) than for others (utilities or MLPs).

The bottom line is that a room full of investors who all claim to use margin of safety can contain a group with vast disagreements on how the MOS is computed, how large it should be and whether it should vary across investments and time.

Myths about Margin of Safety

When talking about value, I am often challenged by value investors on how I control for risk and asked why I don’t explicitly build in a MOS. Those are fair questions but I do think that some of the investors who are most enamored with the concept fundamentally misunderstand it. So, at the risk of provoking their wrath, here is my list of MOS misconceptions.

Myth 1: Having a MOS is costless

There are some investors who believe that their investment returns will always be improved by using a margin of safety on their investments and that using a larger margin of safety is costless. There are very few actions in investing that don’t create costs and benefits and MOS is not an exception. In fact, the best way to understand the trade off between costs and benefits is to think about type 1 and type 2 errors in statistical analysis. If type 1 errors refer to the fact that you have a false positive, type 2 errors reflect the opposite problem, where you have a false negative. Translating this proposition into investing, let’s categorize type 1 errors as buying an expensive stock, because you mistake it to be under valued, and type 2 errors as not buying a bargain-priced stock, because you perceive it wrongly to be over valued. Increasing your MOS will reduce your type 1 errors but will increase your type 2 errors. 

Many risk averse value investors would accept this trade off but there is a cost to being too conservative and  if that cost exceeds the benefits of being careful in your investment choice, it will show up as sub-par returns on your portfolio over extended periods. So, will using a MOS yield a positive or negative payoff? I cannot answer that question for you, because each investor has to make his or her own judgment on the question, but there are simple tests that you can run on your own portfolios that will lead you to the truth (though you may not want to see it). If you find yourself consistently holding more of your overall portfolio in cash than your natural risk aversion and liquidity needs would lead you to, and/or you don't generate enough returns on your portfolio to beat what you would have earned investing passively (in index funds, for instance), your investment process, no matter what its pedigree, is generating net costs for you. The problems may be in any of the three steps in the process: your valuations may be badly off, your judgment on market catalysts can be wrong or you may be using too large a MOS.

Myth 2: If you use a MOS, you can be sloppy in your valuations

Value investors who spend all of their time coming up with the right MOS and little on valuation are doing themselves a disservice. If your valuations are incomplete, badly done or biased, having a MOS on that value will provide little protection and can only hurt you in the investment process (since you are creating type 2 errors, without the benefit of reducing type 1 errors). Given a choice between an investor with high quality valuations and no/little MOS and one with poorly done valuations and a sophisticated MOS, I would take the former over the latter every single time.

I am also uncomfortable with investors who start with conservative estimates of value and then apply the MOS to that conservative value. In intrinsic valuation, conservative values will usually mean haircutting cash flows below expectations, using high discount rates and not counting in growth that is uncertain. In asset-based valuation, it can take the form of counting only some of the assets because they are tangible, liquid or both. Remember that you are already double counting risk, when you use MOS, even if your valuation is a fair value (and not a conservative estimate of value), because that value is computed on a risk-adjusted basis. If you are using a conservative value estimate, you may be triple or even quadruple counting the same risk when making investment decisions. If you are using this process, I am amazed that any investment manages to make it through your risk gauntlets to emerge as a good investment, and it does not surprise me that nothing in the market looks cheap to you.

Myth 3: The MOS should be the same across all investments 

I have always been puzzled by the notion that one MOS fits all investments. How can a 15% margin of safety be sufficient for both an investment in a regulated utility as well as a money-losing start-up? Perhaps, the defense that would be offered is that the investors who use MOS as their risk breakers would not look at companies like the latter, but I would still expect that even in the value investing spectrum, different investments would evoke different degrees of uncertainty (and different MOS).

Myth 4: The MOS on your portfolio = MOS on individual investments in the portfolio

I know that those who use MOS are skeptics when it comes to modern portfolio theory, but modern portfolio theory is built on the law of large numbers, and that law is robust. Put simply, you can aggregate a large number of risky investments to create a relatively safe portfolio, as long as the risks in the individual stocks are not perfectly correlated. In MOS terms, this would mean that an investor with a concentrated portfolio (who invests in three, four or five stocks) would need a much larger MOS on individual investments than one who spreads his or her bets across more investments, sectors and markets.

Expanding on this point, using a MOS will create biases in your portfolio. Using the MOS to pick investment will then lead you away from investments that are more exposed to firm-specific risks, which loom large on an individual company basis but fade in your portfolio. Thus, biotechnology firms (where the primary risk lies in an FDA approval process) will never make your MOS cut, but food processing firms will, for all the wrong reasons. In the same vein, Valeant and Volkswagen will not make your MOS cut, even though the risk you face on either stock will be lowered if they are parts of larger portfolios. 

Myth 5: The MOS is an alternative risk measure

I know that many investors abhor betas, and believe it or not, I understand. In fact, I have long argued that there are replacements available for portfolio theory-based risk measures and that not only is intrinsic value robust enough to work with these alternative risk measures but that the discount rate is not (and should not) be the ultimate driver of value in most companies. That said, there are some in the value investing community who like to use their dislike of betas as a bludgeon against all financial theory and after they have beaten that straw horse to death, they will offer MOS as their alternative risk measure. That suggests a fundamental misunderstanding of MOS. To use MOS, you need an estimate of value and I am not aware of any intrinsic value model that does not require a risk adjustment to get to value. In other words, MOS is not an alternative to any existing risk measure used in valuation but an add-on, a way in which risk averse investors can add a second layer of risk protection.

There is one possible way in which the MOS may be your primary risk adjustment mechanism and that is if you use a constant discount rate when doing valuation (a cost of capital of 8% for all companies or even a risk free rate) and then apply a MOS to that valuation to capture risk. If that is your approach, you should definitely be using different MOS for different investments (see Myth 3), with a larger MOS being used on riskier investments. I would also be curious about how exactly you make this MOS adjustment for risk, including what risks you bring in and how you make the conversion.

Margin of Safety – Incorporating into a Strategy

I would not put myself in the MOS camp but I recognize its use in investing and believe that it can be incorporated into a good investing strategy. To do so, though, you would need to do the following:

1. Self examination: Even if you believe that MOS is a good way of picking investments, it is not for everyone. Before you adopt it, you have to assess not only your own standing (including how much you have to invest, how risk averse you are) but also your faith (in your valuation prowess and that markets correct their mistakes). Once you have adopted it, you still need the effects it has on your portfolio, including how often you choose not to invest (and hold cash instead) and whether it makes a material difference to the returns you generate on your portfolio.
2. Sound Value Judgments: As I noted in the last section, a MOS is useful only if it is an addendum to sound valuations. This may be a reflection of my biases but I believe that this requires intrinsic valuation, though I am willing to concede that there are multiple ways of doing it right. Accounting valuations seem to be built on the twin presumptions that book value is an approximation of liquidation value and that accounting fair value actually means what it says, and I have little faith in either. As for passing of pricing as value, it strikes me as inconsistent to use the market to get your pricing number (by using multiples and comparable firms) and then argue that the same market misprices the asset in question.
3. A Flexible MOS: Tailor the MOS to the investment that you are looking at: There are two reasons for using a MOS in the first place. The first is an acceptance that, no matter how hard you try, your estimate of value can be wrong and the second is that even if the value estimate is right, there is uncertainty about whether the market will correct its mistakes over your time horizon. If you buy into these two reasons, it follows that your MOS should vary across investments, with the following determinants.

• Valuation Uncertainty: The more uncertain you are about your estimated value for an asset, other things remaining equal, the larger the MOS should be. Thus, you should use a smaller MOS when investing in mature businesses and during stable markets, than when putting your money in young, riskier business or in markets in crises.
• Portfolio Tailoring: The MOS that you use should also be tailored to your portfolio choices. If you are a concentrated investor, who invests in a four or five companies, you should use a much higher MOS than an investor who has a more diversified portfolio, and if you the latter, perhaps even modify the MOS to be larger for companies that are exposed to macroeconomic risks (interest rates, inflation, commodity prices or economic cycles) than to company-specific risks (regulatory approval, legal jeopardy, management flux).
• Market Efficiency: I know that these are fighting words to an active investor, red flags that call forth intemperate responses. The truth, though, is that even the most rabid critics of market efficiency ultimately believe in their own versions of market efficiency, since if markets never corrected their mistakes, you would never make money of even your canniest investments. Consequently, you should settle for a smaller MOS when investing in stocks in markets that you perceive to be more liquid and efficient than in assets, where the corrections will presumably happen more quickly than in inefficient, illiquid markets where the wait can be longer.
• Pricing Catalysts: Since you make money from the price adjusting to value, the presence of catalysts that can lead to this adjustment will allow you to settle for a lower MOS. Thus, if you believe that a stock has been mispriced ahead of an earnings report, a regulatory finding or a legal judgment, you should demand a lower MOS than when you invest in a stock that you believe is misvalued but with no obvious pricing catalyst in sight. 

Finally, if MOS is good enough to use when you buy a stock, it should be good enough to use when you sell that stock. Thus, if you need a stock to be under valued by at least 15%, to buy it, should you also not wait until it is at least 15% over valued, to sell it? This will require you to abandon another nostrum of value investing, which is that once you buy a great company, you should hold it forever, but that is not just unwise but is inconsistent with true value investing.

Conclusion

Would I prefer to buy a stock at a 50% discount on value rather than at just below fair value? Of course, and I would be even happier if you made that a 75% discount. Would I feel even more comfortable if you estimated value very conservatively. Yes and I would be delighted if all you counted was liquid assets. That said, I don't live in a  world where I see too many of these investments and when I do, it is usually the front for a scam rather than a legitimate bargain.  That is the reason that  I have never formally used a MOS in investing. I did buy Valeant at $32, because my valuation of the stock yielded $45 for the company. Would I have still bought the stock, if my value estimate had been only $35 or if it was a big chunk of my portfolio? Perhaps not, but I have bought stocks that were priced at my estimated fair value and have held back on investments that I have found to be under valued by 25% or more. Why? That has to wait for my coming post on simulations, since this one has run its course.

YouTube Video


Uncertainty Posts

1. DCF Myth 3: You cannot do a valuation, when there is too much uncertainty
2. The Margin of Safety: Excuse for Inaction or Tool for Action?
3. Facing up to Uncertainty: Probabilities and Simulations

DCF Myth Posts

Introductory Post: DCF Valuations: Academic Exercise, Sales Pitch or Investor Tool

1. If you have a D(discount rate) and a CF (cash flow), you have a DCF.  
2. A DCF is an exercise in modeling & number crunching. 
3. You cannot do a DCF when there is too much uncertainty.
4. It's all about D in the DCF (Myths 4.1, 4.2, 4.3, 4.4 & 4.5)
5. The Terminal Value: Elephant in the Room! (Myths 5.1, 5.2, 5.3, 5.4 & 5.5)
6. A DCF requires too many assumptions and can be manipulated to yield any value you want.
7. A DCF cannot value brand name or other intangibles. 
8. A DCF yields a conservative estimate of value. 
9. If your DCF value changes significantly over time, there is something wrong with your valuation.
10. A DCF is an academic exercise.

DCF Myth 3: You cannot do a valuation, when there is too much uncertainty!

Uncertainty, both imminent and resolved, has been on my mind these last two weeks. I posted my valuation of Valeant on April 20, making the argument that, at least based on my expectations on what could be revealed in the delayed financial filings, the stock was worth about $44, approximately $12 more than the prevailing stock price. Many of you were kind enough to comment on my valuation, and one of the more common refrains was there were too many unknowns on the stock to be taking a stand. In fact, one of the comments on the post was that "regardless of the valuation, a sufficient margin of safety does not exist (on the stock)". On April 21, we got news that Volkswagen had come to an agreement with US authorities on the compensation that they would offer buyers of their cars and a day later, the company announced that it would take an $18.2 billion charge to cover the costs of its emissions misrepresentations. It was a chance for me to revisit my valuation of Volkswagen, in the immediate aftermath of the scandal in October 2015, and take stock of how the the investment I made in the stock then looks, as the uncertainty gets slowly resolved. All through these last two weeks, there were signs that Yahoo's journey, that was starting to resemble the Bataan Death March lately, was nearing its end, as the company reviewed bids for its operating assets. Since it is a stock that I valued almost two years ago (and bought after the valuation) and labeled as a Walking Dead company, I am interested, both financially and intellectually, to see how this end game plays out. As I wrestle with the resolution of uncertainties from the past and struggle with uncertainties in the future on every one of my investments, I thought it would be a good time to look at good and bad ways of responding to I uncertainty in investing and valuation.

The Uncertainty Principle

Uncertainty has always been part of human existence, though it has transitioned from the physical uncertainty that characterized the caveman era to the economic uncertainty that is more typical of today, at least in developed markets. Each generation, though, seems to think that it lives in the age of the greatest uncertainty. That may be partially a reflection of a broader sense of "specialness" that afflicts each generation, where it is convinced that its music and movies were the very best and that it had to get through the biggest challenges to succeed. The other is a variation of hindsight bias, where we can look at the past and convince ourselves that what actually happened should have been obvious before it occurred. I am surprised at how many traders, investors and portfolio managers, who lived through the 2008 crisis, have convinced themselves that November 2008 was not that bad and that there was never a chance of a catastrophic ending.  That said, uncertainty not only ebbs and flows over time but also changes form, making enduring fixes and lessons tough to find. As investors bemoan the rise of uncertainty in today's markets, there are three reasons why they may feel more under siege now than in prior decades:

1. Low Interest Rates: In my post on negative interest rates, I pointed to the fact that as interest rates in many of the leading currencies have dropped to historic lows, risk premiums have increased in both stock and bond markets. The expected return on the S&P 500 in early 2008, before the crisis, was 8% and it remains at about that level today, even though the treasury bond rate has dropped from 4% to less than 2%, but the equity risk premium has risen to compensate. Even though the expected return may be the same, the fact that more of it can be attributed to a risk premium will increase the market reaction to news, in both directions, adding to price volatility.
2. Globalization: Globalization has not only changed how companies and investors make choices but has also had two consequences for risk. The first is that there seem to be no localized problems any more, with anyone's problem becoming everyone's problem. Thus, political instability in Brazil and too much local government borrowing to build infrastructure in China play out on a global stage, affecting stock prices in the rest of the world. The second is that the center of global economic power is shifting from the US and Europe to Asia, and as it does, Americans and Europeans are starting to bear more of world's economic risk than they used to.
   
3. Media/Online Megaphones: As an early adopted of technology, I am far from being a Luddite but I do think that the speed with which information is transmitted around the world has allowed market risks to go viral. It is not just the talking heads on CNBC, Bloomberg and other financial news channels that are the transmitters of these news but also social media, as Twitter and Facebook become the place where investors go to get breaking investing news.

I am sure that you can add other items to this list, such as the disruption being wrought by technology on established businesses, but I am not sure that these are either uncommon or unusual. Every decade has its own disruptive factors, wreaking havoc on existing business models and company values.

The Natural Responses to Uncertainty

Much of financial theory and a great deal of financial practice was developed in the United States in the second half of the last century and therein lies a problem. The United States was the giant of the global economy for much of this period, with an economy on an upward path. The stability that characterized the US economy during this period was unusual, if you look at long term history of economies and markets, and much as we would like to believe that this is because central bankers and policy makers learned their lessons from the great depression, there is the very real possibility that it was just an uncommonly predictable period. That would also mean that the bedrock of financial practice, built on extrapolating from past data and assuming mean reversion in all things financial, may be shaky, and that we have to reevaluate them for the economies that we operate in today. It is unfair to blame the way we deal with uncertainty entirely on the fact that our practices were honed in the United States. After all, it is well chronicled in both psychological annals and behavior studies that we, as human beings, deal with uncertainty in unhealthy ways, with the following being the most common responses:

1. Paralysis and Inaction: The most common reaction to uncertainty, in my experience, is inaction. "There is too much uncertainty right now to act" becomes the refrain, with the promise that action will come when more of the facts are know. The consequences are predictable. I have friends who have almost entirely been invested in money market funds for decades now, waiting for that moment of clarity and certainty that never seems to come. I have also talked to investors who seem to view investing when uncertain as a violation of value investing edicts and have found themselves getting pushed into smaller and smaller corners of the market, seeking elusive comfort.
2. Denial and Delusion: At the other end of the spectrum, the reaction that other investors have to uncertainty is go into denial, adopting one of two practices. The number crunchers fall back on false precision, where they add more detail to their forecasts and more decimals to their numbers, as a defense against uncertainty. The story tellers fall back on story telling, acting as if they have the power to write the endings to every uncertain narrative, when in fact they have little control over either the players or the outcome.
3. Mental Accounting and Rules of Thumb: The brain may be a wondrous organ but it has its own set of tics that undercut investing, when uncertain. As Richard Thaler has so convincingly shown in his work on mental accounting, investors and analysts like to use rules of thumb, often with no basis in fact or reality, when making judgments. Thus, a venture capitalist who is quick to dismiss the use of intrinsic value in a young start-up as too fraught with estimation error, seems to have no qualms about forecasting earnings five years out for the same company and applying a price earnings ratio to those earnings to get an exit value.
4. Outsourcing and Passing the Buck: When stumped for answers, we almost invariably turn to others that we view as more knowledgeable or better equipped than we are to come up with solutions. Cynically, you could argue that this allows us to avoid taking responsibility for investment mistakes, which we can now attribute to consultants, text book writers or that person you heard on CNBC. 
5. Prayer and Divine Intervention: The oldest response to uncertainty is prayer and it has had remarkable staying power. There are large segments of the world where big investment and business decisions are preceded by prayers and divine intervention on your behalf. 

If the first step in change is acceptance, I have come to accept that I am prone to do some or all of the above, when faced with uncertainty, but I have also discovered that these reactions can do damage to my portfolio. 

Dealing with Uncertainty

To reduce, if not eliminate, my unhealthy responses to uncertainty, I have developed my own coping mechanisms that will hopefully push me on to healthier tracks. I am not suggesting that these will work for you, but they have for me, and please feel free to modify, abandon or adjust them to your own needs.

1. Have a narrative: As many of you who read this blog know, I have long believed that a company valuation without a story to bind it together is just numbers on a spreadsheet and a story that uses no numbers at all is a fairy tale. There is another advantage in having a narrative underlie your valuation and tying numbers to that narrative. When faced with uncertainty about specifics, the question that I ask is whether these specifics affect my narrative for the company and if yes, in what way. In my valuation of Volkswagen, right after the diesel emissions scandal, I did not find a catastrophic drop in value for the company because my underlying narrative for Volkswagen, that of a mature business with little to offer in terms of expansion or growth opportunities, was dented but largely unchanged as a result of the scandal. With Valeant, in my November 2015 valuation, I argued that the attention brought to the company by its drug pricing policies and connections to Philidor would result in it having to abandon its strategy of growth driven by acquisitions and growth and to shift to being a less exciting, lower growth pharmaceutical company. That shift in narrative drove the inputs into my valuation and my lower assessment of value. 

2. Categorize uncertainty: Uncertainty can come from many sources and it is useful, when valuing a company in the face of multiple uncertainties, to classify them. Here are my groupings:

Since it is easy to miss some uncertainties and double count others, I find it useful to keep them isolated in different parts of my valuation:

Specifically, in my Volkswagen and Valeant valuations, it was micro risk that concerned me, with some of that risk being continuous (the effect of the diesel emissions scandal on Volkswagen car sales) and some being discrete (the fines levied by the EPA on Volkswagen and the risk of default in Valeant). That is why both companies, at least in my conventional valuations, have low costs of capital, notwithstanding the risky environment, but their values are then adjusted for the expected costs of the discrete events occurring.

3. Keep it simple:  This may seem ironic but the more uncertainty there is, the simpler my valuation models become, with fewer inputs and less levers to move. One reason is that it allows me to focus on the variables that really drive value for the company and the other is that it reduces my need to estimate dozens of variables in the face of uncertainty. Thus, in my valuations of start-up companies, my focus is almost entirely on three variables: revenue growth, operating margins and the reinvestment needed to sustain that growth. 

4. Make your best estimates: As I start making my estimates in the face of uncertainty, I hear the voice in the back of my mind pipe up, saying "You are going to be so wrong!" and I silence it by  reminding myself that I don't have to be right, just less wrong than everyone else, and that when uncertainty is rampant, most investors give up.

5. Face up to uncertainty: Rather than cringe in the face of uncertainty and act like it is not there, I have found that it is freeing to admit that you are uncertain and then to take the next step and be explicit about that uncertainty. In my valuations of tech titans in February 2016, I used probability distributions for the inputs that I felt most shaky about and then reported the values as distributions. Since some of you have been curious about the mechanics of this process, I will take a lengthier journey through the process of running simulations in a companion piece to this post.

6. Be willing to be wrong: If you don't like to be wrong, it is best not  to value companies in the face of uncertainty. However, if you think that Warren Buffet did not face uncertainty in his legendary investment in American Express after the salad oil scandal in 1964 or that John Paulson knew for sure that his bet against the housing bubble would pay off in 2008, you are guilty of revisionist history. There is a corollary to this point and it relates to diversification. As I have argued in my post on diversification, the more uncertain you feel about individual investments, the more you have to spread your bets. It is not an admission of weakness but a recognition of reality.

If you are a value investor, you will notice that I have not mentioned one of value investors' favorite defenses against uncertainty, which is the margin of safety. Seth Klarman is one of my favorite investment thinkers but I am afraid that the margin of safety, at least as practiced by some in the investing community, has become an empty vessel, an excuse for inaction rather than a guide to action in risky times. I will come back to this measure as well in another post in this series.

Conclusion

If you are an active investor, you are constantly looking for an edge, something that you can bring to the table that most other investors cannot or will not, that you can exploit to earn higher returns. As the investing world gets flatter, with information freely accessible and available to almost all investors, and analytical tools that anyone can access, often at low cost, being comfortable with uncertainty may very well be the edge that separates success from failure in investing. There may be some who are born with that comfort level, but I am not one of them. Instead, my learning has come the hard way, by diving into companies when things are most uncertain and by valuing businesses in the midst of market crises, "by going where it is darkest". That journey is not always profitable (see my experiences with Vale as a precautionary note), sometimes makes me uncomfortable (as I have to make forecasts based upon little or bad information), but it is never boring. I am wrong a hefty percent of the time, but so what? It's only money! I am just glad that I am not a brain surgeon!

YouTube Video

Uncertainty Posts

1. DCF Myth 3: You cannot do a valuation, when there is too much uncertainty
2. The Margin of Safety: Excuse for Inaction or Tool for Action?
3. Facing up to Uncertainty: Probabilities and Simulations

DCF Myth Posts

Introductory Post: DCF Valuations: Academic Exercise, Sales Pitch or Investor Tool

1. If you have a D(discount rate) and a CF (cash flow), you have a DCF.  
2. A DCF is an exercise in modeling & number crunching. 
3. You cannot do a DCF when there is too much uncertainty.
4. It's all about D in the DCF (Myths 4.1, 4.2, 4.3, 4.4 & 4.5)
5. The Terminal Value: Elephant in the Room! (Myths 5.1, 5.2, 5.3, 5.4 & 5.5)
6. A DCF requires too many assumptions and can be manipulated to yield any value you want.
7. A DCF cannot value brand name or other intangibles. 
8. A DCF yields a conservative estimate of value. 
9. If your DCF value changes significantly over time, there is something wrong with your valuation.
10. A DCF is an academic exercise.